飞行器机翼设计

1.设计要求

设计一架类固定翼的跨介质飞行器，跨介质飞行器设计要求如表 1.1 所示。

表1.1 跨介质飞行器性能指标

巡航空速	失速速度	最大飞行速度	最大滑行速度	最大潜行速度	最大潜行深度	总重量	续航时间
≥16.67m/s	10m/s	≥33.34m/s	≥5.56m/s	≥2.78m/s	≥5m	约1.5kg	≥30min

2.跨介质飞行器主要参数估算

总体设计的初期完全定好各项参数是比较困难的，而最主要的飞行器设计参数有三个:

飞行器的起飞重量 $W_{T}$（Kg）;
机翼面积 S（m²）;
电机驱动螺旋桨的推力 P（N）；

这三个参数中任意一个出现变化，就会导致整个飞行器的总体设计方案的改动。对上述三个参数进行处理，给出了下面两个相对参数:

翼载荷W/S（kg/m²）；
推重比T/W；

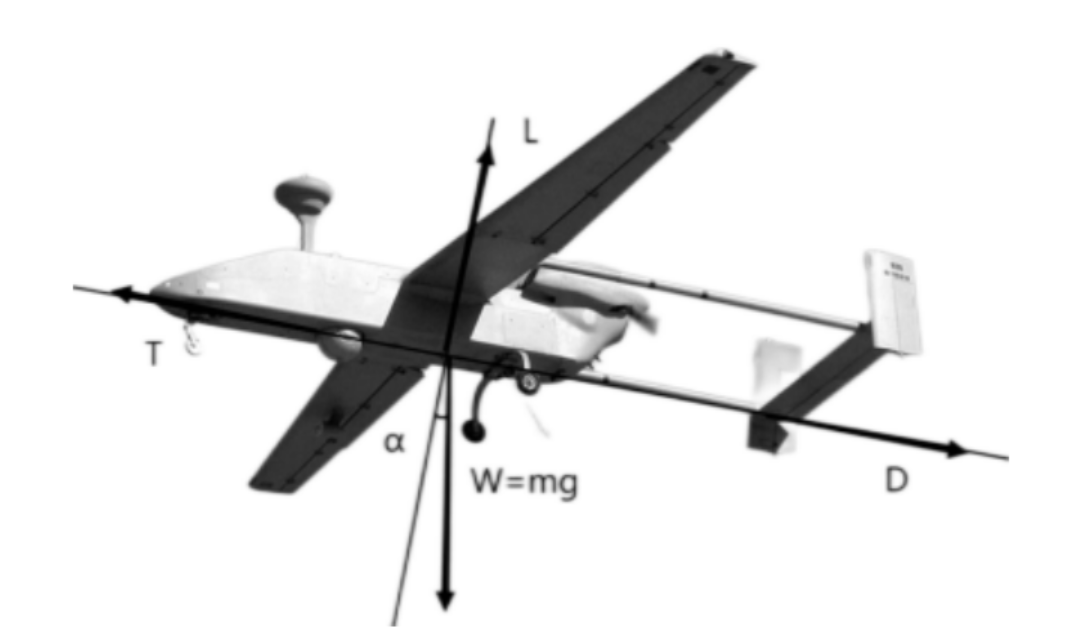
跨介质飞行器在空中匀速平飞时，重力与升力平衡，由平飞要求有：
$$
W＝\frac{1}{2} \rho V_{min}^{2}SC_{Lmax}
$$
式中：W为飞行器重量，

$\rho$为空气密度，

S 为机翼面积，

$V_{min} $为最小平飞速度，

$C_{Lmax}$为最大升力系数

经过变换可得:
$$
\frac{W}{S}＝\frac{1}{2} \rho V^{2}C_{L}
$$
当平飞时，推进器推力等于跨介质航行器阻力
$$
T＝\frac{1}{2}\rho V^{2}SC_{x}
$$
式中：T ——跨介质航行器机翼的推进器推力，N

$ C_{x}$为阻力系数

$ C_{x}$阻力系数可表示为：
$$
C_{x} ＝C_{X_{0} } + C_{X_{i} }
$$
式中：$ C_{X_{0} } $为零升阻力系数，这部分阻力系数与飞行器在没有产生升力时的阻力有关，主要包括形状阻力和摩擦阻力。形状阻力主要由飞行器的几何形状和流体特性决定，而摩擦阻力主要由飞行器表面的粗糙度和空气的粘性特性决定。零升阻力系数与飞行器的设计和制造质量密切相关。

$ C_{X_{i} } $为升致阻力系数，这部分阻力系数与飞行器在产生升力时所引起的阻力有关，主要是诱导阻力。诱导阻力是由于机翼产生升力时在机翼尖端形成的涡旋而产生的阻力。

将（4）式代入（3）式，得到：
$$
T＝\frac{1}{2} \rho V^{2}SC_{X_{0} } +\frac{1}{2} \rho V^{2}SC_{X_{i} }
$$
根据椭圆涡旋理论，我们可以得到以下公式来计算诱导阻力系数（升致阻力系数）：
$$
C_{xi} ＝\frac{ C_{L}^{2}}{π λ e}
$$
其中：

$C_{xi}$：诱导阻力系数
$C_{L}$：升力系数
λ ：展弦比，即翼展与平均弦长之比
e：奥斯瓦尔德效率因子，定义一个机翼效率的数字。椭圆翼效率最高，e为1。

将（6）式代入（5）式，得到：
$$
T＝\frac{1}{2} \rho v^{2} S(C_{x0} +\frac{C_{L}^{2} }{\pi \lambda } )
$$

3.跨介质飞行器MATLAB进行参数估算

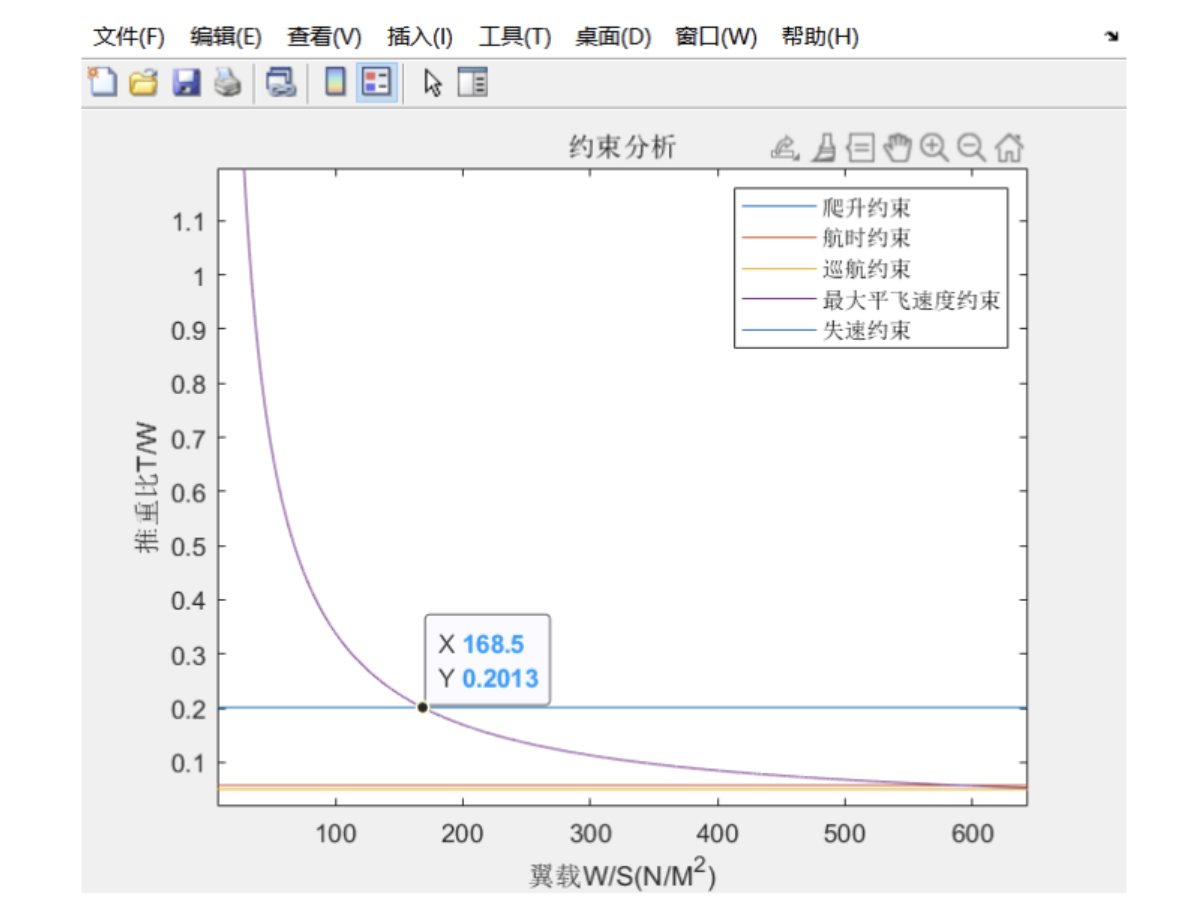
我们选取爬升约束、航时约束、巡航约束、最大平飞速度约束、失速速度约束来作为飞机性能的基本要求。通过参照相关参数和经验公式，确定各个约束方程的相关参数，如下表所示，由此可以绘制出约束曲线族。

a. 爬升约束

飞行器在稳定爬上状态时，采用的推重比计算公式是：
$$
\frac{T}{W} ＝sin\alpha +\frac{(C_{x0} +\frac{C_{L,max}^{2} }{\pi\lambda e } )cos\alpha }{C_{L,max} }
$$
式中：$C_{x0}$为飞行器的零升阻力系数，$C_{L,max}$为飞行器的最大升力系数，α为最大爬升角， λ为展弦比，e为奥斯瓦尔德效率因子。

b. 航时约束

螺旋桨飞机航时最大时的翼载可以用下列公式进行计算：
$$
\frac{W}{S} ＝\frac{1}{2} \rho v^{2} \sqrt{3\pi \lambda eC_{x0} }
$$

c. 巡航速度约束

飞行器在巡航时，处于水平匀速飞行状态。这个时候飞行器的重量等于作用在飞行器上的升力，而推力等于阻力，所以推重比等于升阻比（或升力系数和阻力系数的比值）的倒数，其计算公式如下：
$$
\frac{T}{W} ＝\frac{C_{x0} +\frac{C_{L}^{2} }{\pi \lambda } }{C_{L}}
$$

d. 最大平飞速度约束

推重比也可以根据最大平飞速度来确定。如果能够得到最大平飞速度和翼载，就能计算出所需要的推重比.在水平飞行状态下,推力T需要克服飞行阻力。根据阻力公式，阻力D可以表示为：D = 1/2 * ρ * V_max^2 * C_x * S，其中 S 为机翼面积。为了计算推重比，需要将推力与重量之比表示为阻力与重量之比。因此，需要将阻力公式中的机翼面积S用重量W和翼载荷（W/S）表示。由于 W/S = W / S，可以得到 S = W / (W/S)。
$$
\frac{T}{W} ＝\frac{\frac{1}{2} \rho V {max}^{2} C{x} }{\frac{W}{S} }
$$
式中：$V_{max}$为飞行器的失速速度；$C_{x}$为飞行器的阻力系数。

e.失速速度约束

由飞行器水平飞行时升力等于飞机的质量可以得到翼载表达式:
$$
\frac{W}{S}＝\frac{1}{2} \rho V_{S}^{2}C_{L,max}
$$
式中：$V_{S}$为飞行器的失速速度。

约束类型	约束曲线公式	参数选择
爬升约束	$\frac{T}{W} ＝sin\alpha +\frac{(C_{x0} +\frac{C_{L,max}^{2} }{\pi\lambda e } )cos\alpha }{C_{L,max} }$	α=8°;$C_{x0}$ =0.01;$C_{L,max}$=1.4;λ=8;e=1
航时约束	$\frac{W}{S} ＝\frac{1}{2} \rho v^{2} \sqrt{3\pi \lambda eC_{x0} }$	$\rho$=1.226;v=16.67;λ=8;e=1;$C_{x0}$ =0.01
巡航速度约束	$\frac{T}{W} ＝\frac{C_{x0} +\frac{C_{L}^{2} }{\pi \lambda } }{C_{L}}$	$C_{x0}$ =0.01;$C_{L}$=1;λ=8
最大平飞速度约束	$\frac{T}{W} ＝\frac{\frac{1}{2} \rho V {max}^{2} C{x} }{\frac{W}{S} }$	$\rho$=1.226;$V_{max}$=33.34
失速速度约束	$\frac{W}{S}＝\frac{1}{2} \rho V_{S}^{2}C_{L,max}$	$V_{S}$=10;$C_{L,max}$=1.4

由上图可以得出，翼载荷为 168.5N/m^2^，即17.194kg/m^2^,推重比在 0.2013 以上。

4.总体布局设计

由于平直机翼有低速性能良好而且升阻比较高的优点,故采用常规的平直梯形机翼。

机翼的气动特性受到机翼平面几何参数包括翼面积 S、展弦比$\lambda $ 、根梢比η 等的影响。其中，展弦比的变化将影响机翼的气动导数，如诱导阻力系数$ C_{X_{i} } $ 、零升阻力系数$ C_{X_{0} } $ 和升力线斜率$C_{y}^{α} $等，增大展弦比将在减小机翼诱导阻力的同时增大升阻比；而减小展弦比可以减小机翼根部的弯矩、减轻结构重量，从而有利于承力构件的布置和内部容积的利用，与此同时也可以防止大迎角时的翼尖失速。综合考虑各方面因素选取展弦比$\lambda $=8。由初始设定和前文计算可知：预估翼载荷$W_{T}$ /S 为17.194kg/m^2^ ，飞行器的最大起飞重量为 1.5kg，则暂定的梯形机翼面积为S=0.0872m^2^ 。

接下来，我们需要用展弦比（$\lambda $）和机翼面积（S）来计算翼展（b）。展弦比的公式为：
$$
\lambda = b² / S
$$
翼展b ≈ 0.835 m

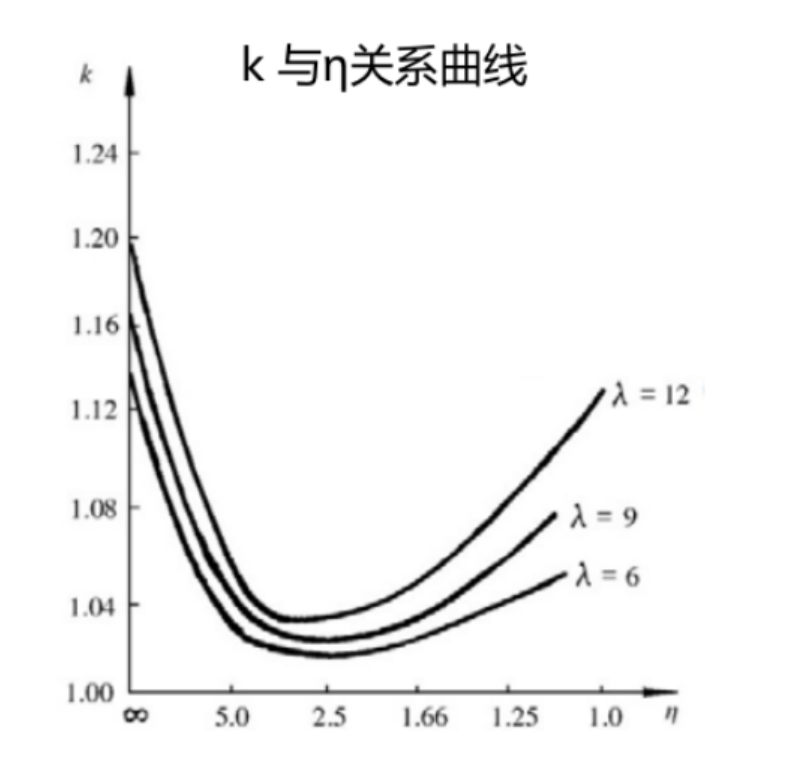
接着确定机翼的根梢比η ，由于设计无人机巡航速度为 16.67m/s，需要考虑机翼诱导阻力的影响，机翼的诱导阻力可以表示成
$$
C_{xi} ＝K\frac{ C_{L}^{2}}{π λ }
$$
当展弦比为定值时，系数 k 是关于根梢比的函数，由 k 与根梢比η 的关系曲线,即查找资料得到在η =1.25 时 k 的值较为理想，且机翼上的气动载荷分布也最接近椭圆形，其余部件尺寸也较为合理。

根据机翼的梯形面积公式和转换后的根梢比的公式：
$$
S = (c_{root} + c_{tip}) * b / 2
$$

$$
c_{tip} = c_{root} / η
$$

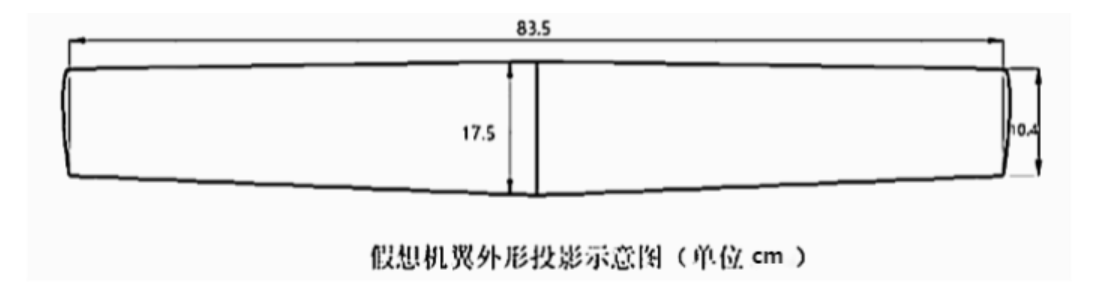
所以，翼根处弦长约为0.175 m，翼梢处弦长约为0.140 m，机翼整体平均气动弦长约为0.104 m。

翼型选择

一般情况下，翼型的选择需满足下列条件：

（1）最大升力系数尽可能大；

（2）在设计升力系数点的阻力系数应尽量小；

（3）在设计升力系数附近，应具有一段尽量平直的低阻区，防止飞机速度变化时阻力产生

较大的波动；

（4）可用迎角范围尽量大以防止失速，且巡航状态下的迎角应尽量远离失速迎角；

（5）相对厚度不能太小，以免机翼付出结构重量上的代价；

（6）翼型的零升力矩系数不能太大，以免引起太大的配平力矩。

雷诺数计算公式：
$$
R_{e} ＝\frac{\rho vD}{u}
$$
式中，$\rho$ 为空气密度，u 为空气粘度，$\rho$ =1.226*kg /m^3^ ，*u =$1.79\times 10^{-5} N\cdot s/m^{} $均为常数；

v 为空气流速，根据巡航速度，取 16.67 m/s； D 为特征尺寸，这里取平均气动弦长，即0.104m。带入数据，算得雷诺数$R_{e}$约为 118743。

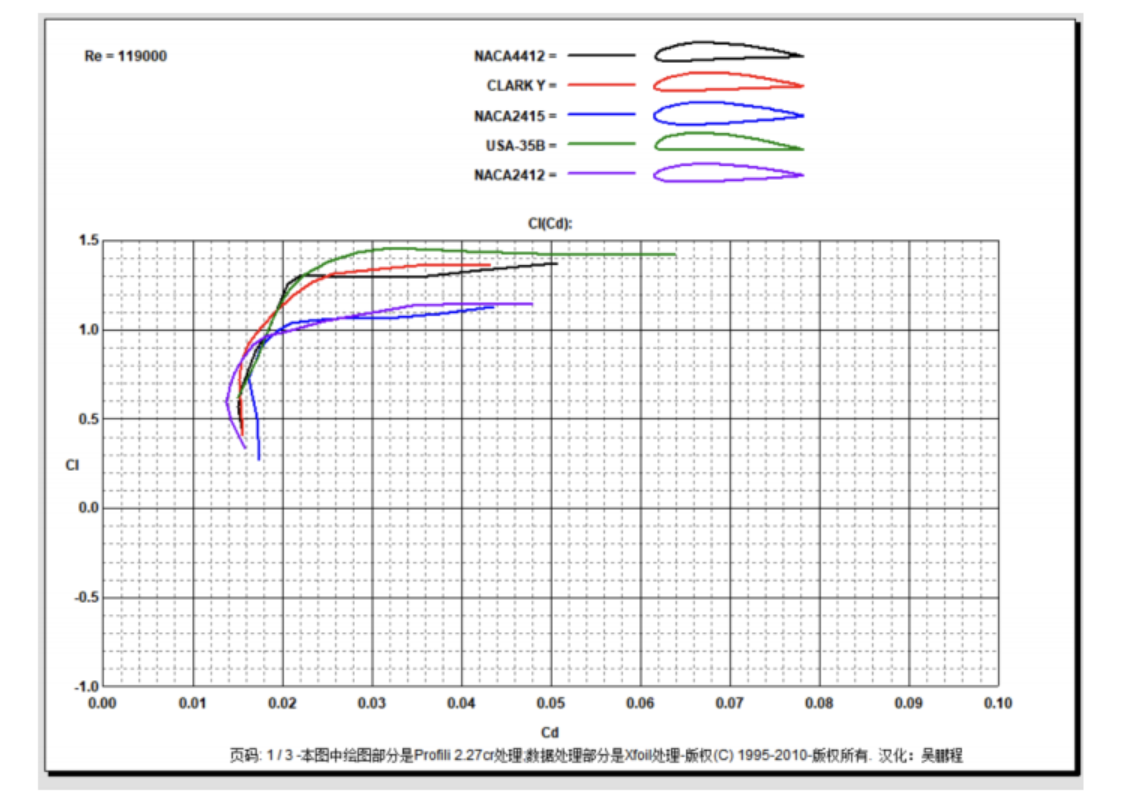
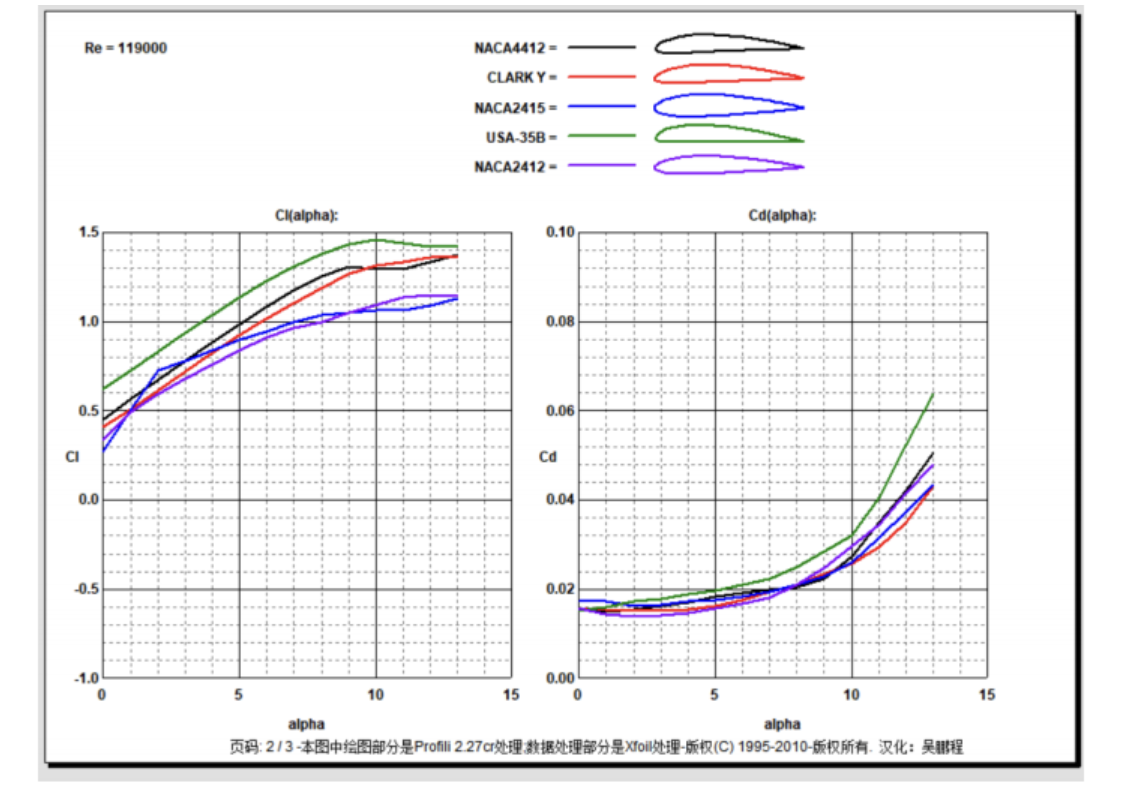
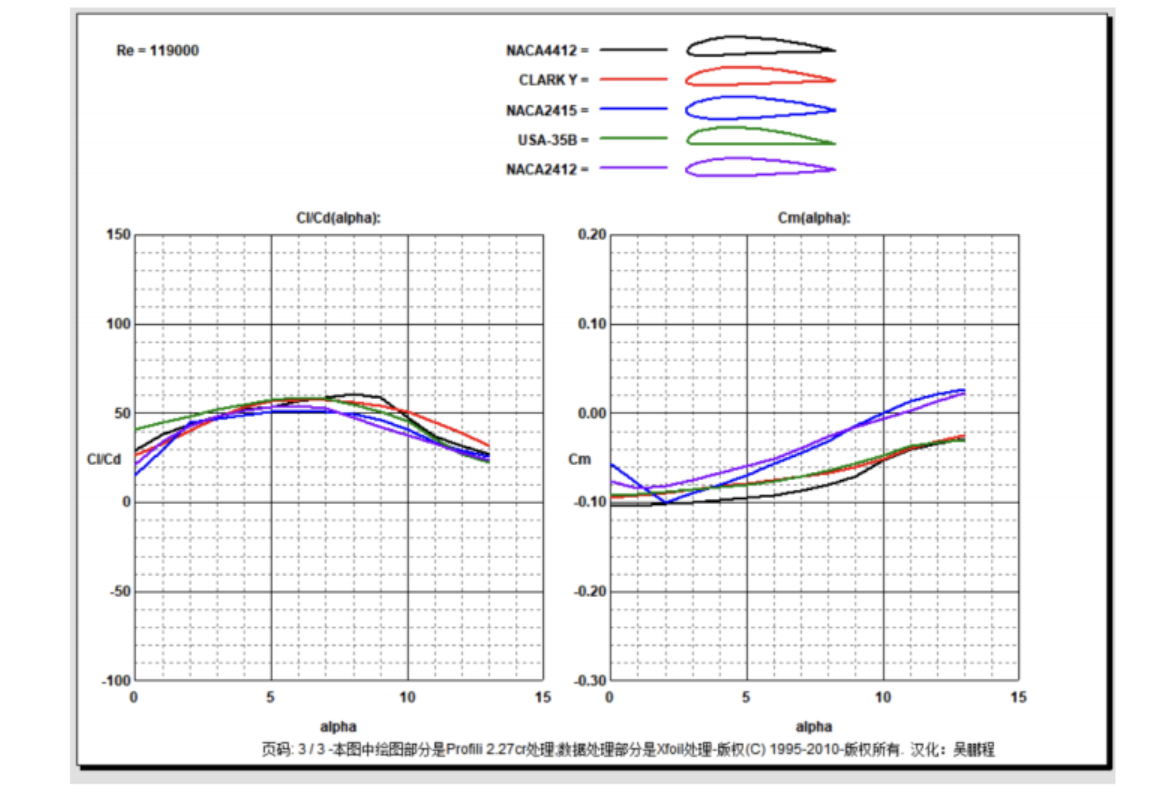
五种翼型的升力系数、阻力系数、升阻比系数和俯仰力矩系数曲线图。

NACA4412(翼型的相对弯度为4%，最大弯度位置在弦长的0.4，相对厚度为12%)；

CLARK Y( 翼型的相对弯度为3.43%，最大弯度位置在弦长的0.42，相对厚度为11.71%);

NACA2415(翼型的相对弯度为2%，最大弯度位置在弦长的0.4，相对厚度为15%)；

USA-35B(翼型的相对弯度为3.19%，最大弯度位置在弦长的0.3，相对厚度为11.61%)；

NACA2412(翼型的相对弯度为2%，最大弯度位置在弦长的0.4，相对厚度为12%)；